Tracking Timelapse

I've put the below primary mirror offset compensation calculations in place, and the rig it tracking well! I made a little timelapse with my webcam behind a pair of sunglasses to prevent overexposure outside.

Tentative Solution to the Offset Mirror Problem

After tackling the cad model in a different way it became clear that the tips of the incoming ray vectors all lay on a circle offset from the circle traced by the centre of the elevation mirror. Knowing this and using some similar triangles I came up with these two equations:

a_z = sin^-1(sin(o_ff)/cos(e))

e_m = tan^-1(tan(o_ff).tan(e)/(sin(a_z) + tan(o_ff).cos(a_z)))

where :

a_z            =             additional azimuth angle added by primary mirror

e_m           =             required elevation of the primary mirror

o_ff           =             offset of the primary mirror from centre

e             =             calculated elevation of the sun

Now the required machine position can be calculated from the elevation and azimuth angles of the sun.

The Source of the Error

Because of the way the primary mirror is offset to prevent shadow being cast onto it from the secondary mirror, it turns out a few complications occur. The adjustment of the primary (elevation) mirror angle effects the azimuth alignment because the reflection plane is not vertical (as it would be if both mirrors were in line). To solve this I need to be able to calculate the two angles marked 'x' and 'y' from the elevation angle E and the mirror offset (currently 18.4deg). I know that the angles 'a' are equal (this is the path of a ray in the plane of reflection).

I have had a go at this but so far am struggling with the derivation. I assumed that the solid lines were of known length (1 for convenience) but this may not be necessary. If anyone feels inspired please give it a crack and let me know how you get on!

I have finally got the psa algorithm to match the NREL code. Not really sure why I got the errors in the previous post but I suspect it was to do with the inputs I gave the NREL calculator, and not with the simpler psa code. Anyway now I'm getting results that match within ~0.5deg. However I am still having issues with my rig drifting out of alignment over time.

I did a little experiment today and set up a sundial with a thin vertical stick in the centre. I marked the position of the shadow with the current calculated azimuth value and waited for the calculated angle to move 30deg (2hours from 1:30 to 3:30).

The rig tracked nicely around 30deg but had over-rotated and was casting a shadow. When I came to measure the new shadow position on the sundial it was only about 20deg from the old mark... So the results that I'm getting from both NREL and the psa algorithms aren't matching what's happening in the real world.

I have a new piece of code from gabriel over at http://www.cerebralmeltdown.com/, which works from tabulated data. I'll give that a go and hope for the best.

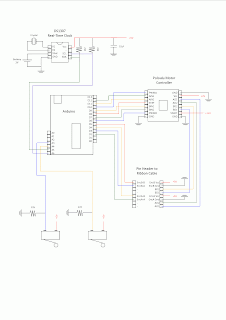
Finalised Circuit in Place

I've just finished transferring my prototype bread board circuit to a more permanent soldered perf-board setup. Been having issues with bad connections here and there so this should finally sort that out.

Also added a circuit diagram page done quickly in publisher.

Sun Position Calc Error Checking

I've run through a little accuracy test of the sun position code I'm using right now, as provided by Mowcius. To check the accuracy I compared results calculated by Mowcius' code and the NREL online solar position calculator solpos (uncertainty of +/- 0.01 degrees).

Results were calculated every 10 minutes for the 11th of November using location data - Longitude = 172, Latitude = -39.

Here is the plot showing the error during the day:

Turns out Mowcius' code is not extremely accurate. But the errors are somewhat consistent and the results for each calculation could be improved, for this day at least, by adding constants (Elevation -2deg and Azimuth +4deg say). Hopefully I can track down a more accurate position calculator, but right now at least I know how much error to expect from the calculation.

For my first post I'd like to share this video which shows one of the first tests of both the tracking calculation and positioning functions. The azimuth (horizontal rotation) axis takes a few seconds to settle at the target position, and the movement of the elevation mirror is a bit jerky, but it feels great to have an almost functional test setup running finally.